In this post, I will go over the SVM-related questions we have dicussed about last Friday. A scanned version of all the 6 questions is available here. Please refer to it while you are skimming through this post. For obvious reasons, Q3 is let go since it’s related to Logistic Regression.

Q1 and Q2 - Understanding the Boundary

For the linearly separable SVM, recall that you are supposed to find such a hyperplane so that it devides all data points in the training set $T= \{(x_1, y_1), ..., (x_N, y_N)\}$ into two classes $\{+1, -1\}$.

$$w^* \cdot x + b^* = 0$$

And its classifier function

$$f(x) = sign(w^* \cdot x + b^* )$$

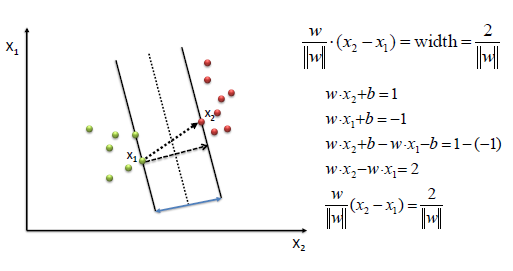
We want to maximize the gap, which is equivalent to minimizing $\frac{1}{2}w\cdot w$, where the so-called support vectors are the sample points that sit right on the ‘river banks’, as such points satisfy

$$y_i(w^* \cdot x_i + b^*) - 1 = 0$$

And a large C penalty coefficient simply means to make sure the gap width is as large as possible.

Q4 ~ Q6 - The Kernel Trick and RBF

Just in case you lose track of the questions, here they are.

Kernel functions are not projection. The $\phi$s are. Kernel functions return scalar values.

The $\phi$s take care of projecting your original data points x’s to a higher dimension feature space, but we don’t need to know(and it’s hard to define) what $\phi$s exactly are. Remember that kernel function regarding two vectors is equal to an implicit dot product that

$$K(x_1, x_2) = \phi(x_1) \cdot \phi(x_2)$$

And in Q4 you are supposed to represent all $\phi$s in the format of K’s.

For Q5 and Q6, given the RBF kernel $K(x_i, x_j) = \exp(-\frac{1}{2})\lVert x_i - x_j \rVert^2$, we can easily get that:

$$K(x_i, x_i) = 1\\ K(x_i, x_j) > 0$$

Since $K(x_i, x_j)$ is a monotonic projection of the Euclidean distance $\lVert x_i - x_j \rVert$. This means for whatever that is the closest to $x_i$ in the lower-dimensional input space, its projection is still the closest to the projected $\phi(x_i)$ in the higher-dimensional feature space.