In this post, I will go over some limitations of the k-means algorithm. To better understand the algorithm, I highly recommend you look into Stanford’s CS229 course note on clustering.

K-means in two steps

So basically speaking, k-means is one of the many unsupervised clustering algorithms to help each one of the data points find their group. The number of clusters, k, is fixed as a given.

• Initialization: Randomly choose k points as initial centroids. ($\mu_1, \mu_2, ... \mu_k$)
• Step 1: Assign each point $x_i$ to its closest centroid in Eucleadian distance. (The $\mu$s don’t change.)
• Step 2: Update the centroids by taking the mean of each cluster. (The cluster boundaries don’t change.)
• REPEAT Step 1 and Step 2 until convergence (when the points no longer switch their clusters in Step 1).

What k-means utilizes here is called Coordinate Descent. The error is bound to converge. But since the SSE (Sum of Squared Error) we aim to minimize is non-convex, we will reach some local minima instead of the global minimum.

$$SSE = \sum^{k}_{i=1} \sum_{x \in C_i} distance^2(\mu_i, x)$$

Limitations of K-means

K-mens is not perfect. It is incapable when it comes to the following situations. Most the following graphs are from the offical textbook notes of Introduction to Data Mining by Tan, Steinbach, and Kumar.

Outliners

OCD trigger warning (assuming k=4).

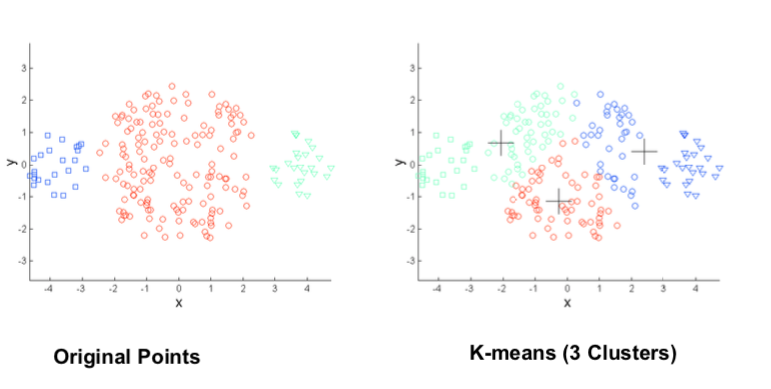
Different Cluster Sizes

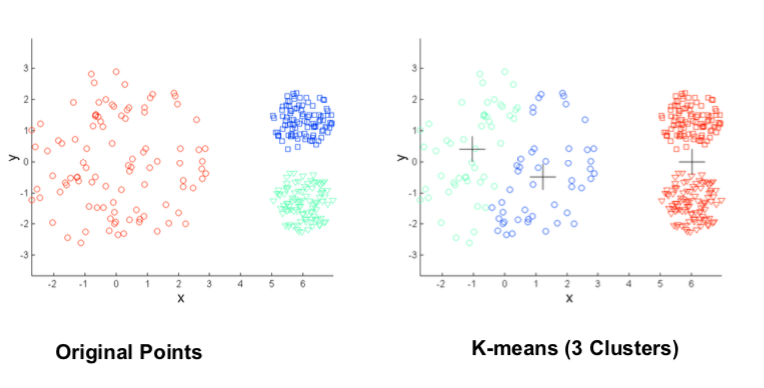
Different Cluster Desities

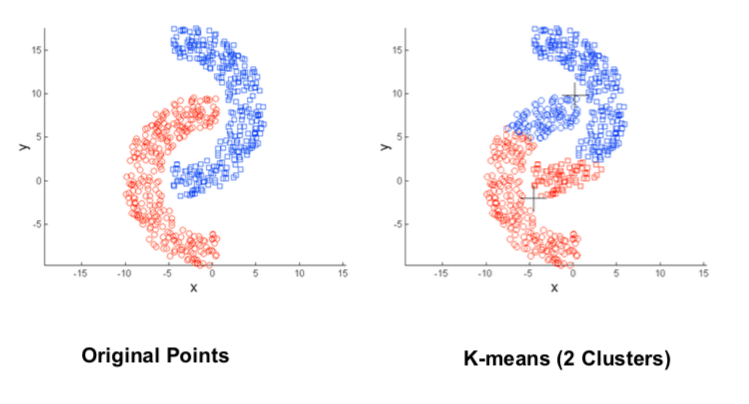
Non-globular Cluster Shape

A universal approach to overcome such limitations is to start with a large k, then combine the smaller clusters. In this sense, choosing an appropriate k and the initial centroids plays big parts, which may affect the local minimum we eventually converge into.